このブログは芝浦工業大学数理科学研究会の新入生に向けて作成された記事です。 誤り・不備があった場合、Twitter等でご指摘いただけると幸いです。

巡回セールスマン問題って？

ついに出た巡回セールスマン問題！#リケ恋 pic.twitter.com/rJTPxIhXyI

— ＼最新15巻発売!／【公式】マンガ＆アニメ「理系が恋に落ちたので証明してみた。」 (@rikeigakoini) January 24, 2020

これ以上知りたいので自分で勉強します。

巡回セールスマン問題(Traveling Salesman Problem)とは、与えられた都市の集合に対して、全ての都市を一度だけ訪れ、出発点に戻る最短経路を求める問題です。 具体的に、都市間の距離が与えられるので、全ての都市を一度だけ訪れ出発点に戻る最短経路を求める問題です。

$N$個の都市があるとき、全ての都市を巡回して戻ってくるルートは $N!$ 通り存在します。 $N=10$ のときは $10! = 3628800$ 通り、$N=20$ のときは $20! = 2432902008176640000$ 通りと、 都市の数が増えるにつれて、全ての経路の数が階乗の形で増加してしまうため、最適解を求めることが非常に困難な問題です。 愚直に全ての経路を試して最短経路を求めようとすると、 $\Omega(N!)$ 掛かってしまいます。

この問題は、輸送や物流、電気回路設計など、現実の様々な問題に応用されています。例えば、配達員が複数の配達先を巡回するときや、電気回路の部品を最小の距離でつなぐときなどに使われます。

今回は、巡回セールスマン問題に対して厳密解を求める手法(Algorithm的なアプローチ)と、近似解を求める手法(Heuristic的なアプローチ)について解説します。

Algorithm的なアプローチ

先述した"愚直に全ての経路を試し、最短経路を求める"という手法だと $\Omega(N!)$ 掛かりますが、 ヘルドカープのアルゴリズムを用いると、 $O(N^2 2^N)$ で解くことができます。

動的計画法

ヘルドカープのアルゴリズムは、動的計画法を用いた手法です。まずは動的計画法について説明します。

動的計画法とは、解きたい問題を小さな部分問題に分割し、それらの部分問題の解を用いて、元の問題の解を求める手法です。

動的計画法の例として、うさぎのつがい問題を考えます。うさぎのつがい問題とは、次のような問題です。

1つがいのうさぎは産まれて2ヶ月後から、毎月1つがいのうさぎを産むとします。今、産まれたばかりの1つがいのうさぎがいます。$n$ ヶ月後には、うさぎは合計何つがいになっているでしょうか？ (1つがいとは、オスとメスの組のことです。)

$n$ ヶ月後のうさぎの数を $F_n$ と書くことにします。$F_n$ の値を求める問題を考えます。 問題より、$F_1 = 1$ です。また、このうさぎのつがいは生まれたばかりなので、翌月には産むことができないため、$F_2 = 1$ です。 $n \geq 3$ のときについて考えます。$n$ ヶ月後のうさぎのつがいの数は、$n - 1$ ヶ月後の新たに生まれたうさぎのつがいの数と、元からいるうさぎのつがいの数がわかればそこから求めることができます。

• $n - 1$ ヶ月後に新たに生まれたうさぎのつがいの数は、$n - 2$ か月後のうさぎのつがいの数との差です。すなわち、$F_{n-1} - F_{n-2}$ です。
• $n - 1$ か月後に元からいるうさぎのつがいの数は、$n - 2$ か月後のうさぎのつがいの数です。すなわち、$F_{n-2}$ です。 $n$ か月後のうさぎのつがいの数について考えます。$n - 1$ か月後に新たに生まれたうさぎのつがいは子を産むことができませんが、元からいるうさぎのつがいは子を産みます。よって数が2倍になります。 よって、$n$ か月後のうさぎのつがいの数は、$F_n = (F_{n - 1} - F_{n - 2}) + 2F_{n - 2} = F_{n - 1} + F_{n - 2}$ と計算することができます。

これより、解きたい問題「$n$ か月後のうさぎのつがいの数」を小問題「$n - 1$ か月後のうさぎのつがいの数」と 「$n - 2$ か月後のうさぎのつがいの数」に分割することができました。 分割した問題について、また同様に分割することで、最終的には解きたい問題 「$n$ か月後のうさぎのつがいの数」を求めることができます。 このような手法を、動的計画法と呼びます。

(じつは $n$ か月後のうさぎのつがいの数は、フィボナッチ数列の第 $n$ 項目の値と一致する！)

ヘルドカープのアルゴリズム

$N$ 個の都市がある巡回セールスマン問題、つまり、 頂点集合 $V = \{1, 2, \ldots, N \}$ に対して、$1$ からスタートし $V$ の頂点をすべて訪れて $1$ に戻る最短経路を求める問題を考えます。 ここで、これが解ければ、$N$ 個の都市を巡回する最短経路が求められます(全ての頂点を通るため、頂点$1$からスタートする最短経路を考えてもよいです)。

以下、頂点 $u$ から頂点 $v$ への距離を $d_{u, v}$ と表します。

$$ f(S, v) \coloneqq 1 からスタートし、S の各頂点を全て訪れて v にいる時の最短経路の長さ $$

という関数を考えます。ここで、$S$ は頂点集合 $V$ の部分集合であり、$v \in S$ とします。 この関数の値が求められたならば、解きたい問題の解は $$ \min_{v \in V} \{ f(V, v) + d_{v, 1} \} $$ で求めることができます。

この関数 $f(S, v)$ を求めることを考えます。 まず、 $f(\{1\}, 1) = 0$　です。1からスタートして今1にいるので、距離は $0$ です。

$S$ が $\{1\}$ でないときの $f(S, v)$ の値を考えます。$f(S, v)$ の値は「$S$の各頂点を全て訪れて $v$ にいる時の最短経路の長さ」でした。

$S \backslash \{v\}$ ($S$から$v$を除いた集合) について考えます。$s \in S \backslash \{v\}$ とすると、 $f(S \backslash \{v\}, s)$ は「$S \backslash \{v\}$ の各頂点を全て訪れて $s$ にいる時の最短経路の長さ」です。この状態から $v$ に移動することを考えると、 その値 $f(S \backslash \{v\}, s) + d_{s, v}$ は「$S$の各頂点を全て訪れて $v$ にいる最短経路の長さの候補」になります。よって、求める値は候補のうちで最も小さいものになるので、 $$ f(S, v) = \min_{s \in S \backslash \{v\}} \{ f(S \backslash \{v\}, s) + d_{s, v} \} $$ と求めることができます。

ここでは $S$ を集合としましたが、コードを書くときには少し工夫をします($N \leq 20$ 程度とします)。 $S$ をbitで表現します。例えば $S = \{1, 3, 5\}$ ならば、$S$ のbit表現は $10101$ です。 bitで表現することにより、様々な操作が簡単に行えます。以下、C++での例を挙げます。

• a << b : $a$ を左に $b$ bitシフト 例えば (10101 << 2) == 1010100
• a & b : $a$ と $b$ のbitごとの論理積 例えば (10101 & 11001) == 10001 (各bitが1と1のときのみ1)
• a | b : $a$ と $b$ のbitごとの論理和 例えば (10101 | 11001) == 11101 (各bitが0と0のときのみ0)
• a ^ b : $a$ と $b$ のbitごとの排他的論理和 例えば (10101 ^ 11001) == 01100 (各bitが異なるときのみ1)

これらを用いると、例えば $S \backslash \{v\}$ は S ^ (1 << v) と表せたり、$S$ に $v$ が含まれているかどうかを S & (1 << v) と表せたりします。

実際にこれを実装すると、次のようになります。問題はAtCoderの典型アルゴリズム問題集にあります。

https://atcoder.jp/contests/typical-algorithm/tasks/typical_algorithm_c

問題

$N$ 個の都市があり、$0, 1, \ldots, N$ と番号付けられている。全ての異なる2都市の間には道が存在し、都市 $i$ から都市 $j$ に移動するときのコストは $A_{i, j}$ である。あなたは今都市 $0$ にいる。ここから都市 $0$ 以外の都市をちょうど1度ずつ訪れ、最後に都市 $0$ に戻ってくる経路を創りたい。そのような経路における合計コストの最小値を求めよ。

回答

#include <bits/stdc++.h>
using namespace std;

int main() {

    // 入力
    int N; cin >> N;
    vector A(N, vector<long long>(N));
    for (int i = 0; i < N; ++i) {
        for (int j = 0; j < N; ++j) {
            cin >> A[i][j];
        }
    }

    // dp[S][v] := 1 からスタートし、S の各頂点を全て訪れて v にいる時の最短経路の長さ
    // (記事では f と置いていたが、ここでは dp と書く)
    // 大きい値で初期化しておく
    vector dp(1 << N, vector<long long>(N, 1e18));
    dp[1][0] = 0;

    for (int S = 0; S < (1 << N); S++) {
        for (int i = 0; i < N; i++) {
            for (int j = 0; j < N; j++) {
                if (S & (1 << j)) {
                    dp[S][i] = min(dp[S][i], dp[S ^ (1 << i)][j] + A[j][i]);
                }
            }
        }
    }

    // 答えは dp[(1 << N) - 1][i] + A[i][0] の最小値
    long long ans = 1e18;
    for (int i = 0; i < N; i++) {
        ans = min(ans, dp[(1 << N) - 1][i] + A[i][0]);
    }

    cout << ans << endl;

}

この手法を用いることで、頂点数が $N$ の巡回セールスマン問題を $O(N^2 2^N)$ で解くことができます。

Heuristic的なアプローチ

ヘルドカープのアルゴリズムを用いると $N \leq 20$ 程度までの問題に対しては解くことができますが、それ以上になると(指数的に実行時間が長くなるため)解くことが困難になります。

今まで厳密解を求めることを考えていましたが、今度は近似解を求めることを考えます (ここでいう近似解とは、「最適解には達しないが、比較的良い解」のことです)。

山登り法

ある問題に対して、現在の解を少し変化させて良くなったら採用し、これを繰り返すことで答えをどんどん良くしていく手法を山登り法といいます。

巡回セールスマン問題に対しても、山登り法を用いることで、近似解を求めることができます。 具体的に、以下のような手順で近似解を求めます。

1. ランダムな順列を生成する(初期解)
2. 以下を繰り返す
   1. 現在の解を少し変化させる(近傍解)
   2. 現在の解より近傍解の方が良ければ、近傍解を現在の解とする

ここでは、近傍解を求める方法を「ランダムに2つの都市を選び、訪れる順番を入れ替える」として考えてみます。

ランダム2点間swapの山登り pic.twitter.com/EfucnjfXBo

— きょ (@Kyo_s_s) April 16, 2023

ランダムな初期解から時間が経つにつれて、解が良くなっていくことがわかります。これが山登り法です。

山登り法は、最適解に到達する保障はありませんが、近傍解を効率的に生成することができる場合、比較的シンプルに近似解を求めることができます。 しかし、局所最適解に陥りやすかったり、初期解や近傍解の生成方法によっては良い解にたどり着けない場合もあります。

2-opt

先ほどは近傍解を作る方法を「ランダムに2つの都市を選び、訪れる順番を入れ替える」として考えましたが、この他にも様々な近傍解の作り方が考えられます。

今度は近傍解を2-optという手法を用いて求めてみます。 2-optとは、現在の解の中で2つの都市を選び、その間の順番を逆にすることで近傍解を作ります。

例えば、以下のような解があったとします。

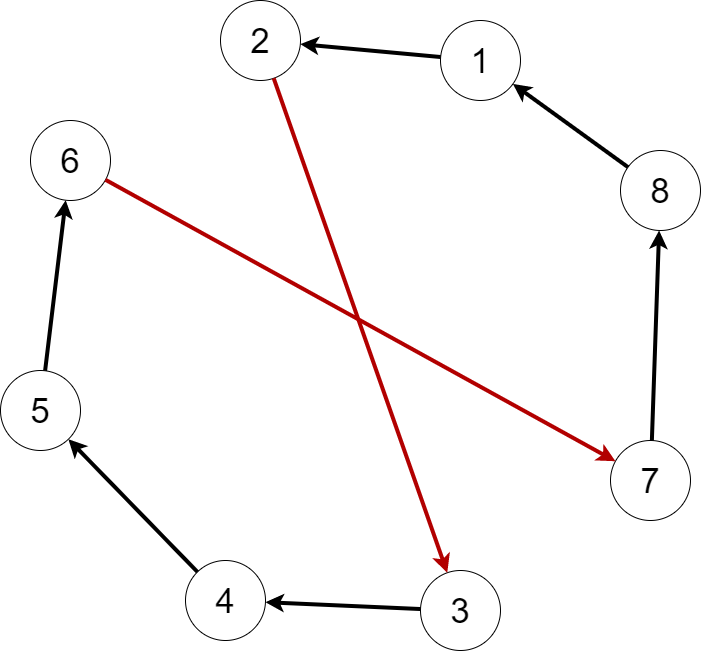
1-2-3-4-5-6-7-8 という順番で訪れる解です。2-3の辺と6-7の辺が交差しています(赤い辺です)。 ここで、2の次に6へ訪れ、5,4,3,7の順で訪れる、つまり 1-2-6-5-4-3-7-8 という解を考えます。

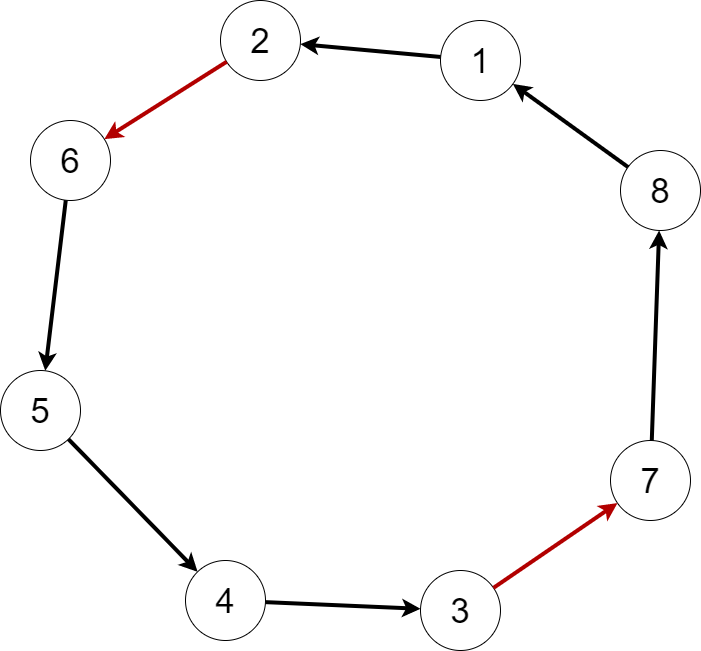
訪れる順序を一部逆にするだけで、交差していた箇所が解消され、距離が短くなりました！

このように、訪れる順序の一部を逆にするような近傍会を使い山登り法を行う手法を2-opt法といいます。 実際に2-optを用いて山登り法を行うと、以下のようになります。

2-opt pic.twitter.com/5Pimy9yENT

— きょ (@Kyo_s_s) April 15, 2023

2-optを用いることで、「ランダムに2つの都市を選び、訪れる順番を入れ替える」を近傍解の生成方法として用いた場合と比べて、より良い解を求めることができることがわかります。

まとめ

• 巡回セールスマン問題とは、$N$ 個の都市を全て訪れて戻ってくるような最短経路を求める問題！
• $N$ が大きくなると経路の数が爆発的に増えてしまうため、厳密解を求めることが難しい！
  • ヘルドカープのアルゴリズムを用いると、$N \leq 20$ 程度までの問題に対しては解くことができるようになる！
• 近似解を求めることもできる！
  • 山登り法を用いると、ランダムな初期解から時間が経つにつれて、解が良くなっていくことがわかる！
  • 2-opt法など、近傍解を効率的に生成することができるとよりよい近似解を求めることができる！