桁DPを理解する
理解できていません
決定性有限オートマトン
入力された文字列がある規則に従っていれば受理, 従っていなければ拒否をする機械です.
まず, アルファベットと文字列を定義します.
定義
適当な文字あるいは記号の空でない有限集合$\Sigma$ をアルファベットといい, $\Sigma$ の元からなる有限列を文字列という.
有限列$x = (x_1, x_2, \cdots, x_n)~(x_i \in \Sigma)$ を文字列として考える場合, $x = x_1x_2\cdots x_n$ と括弧やカンマを書かずに文字を並べて記し, これをアルファベット$\Sigma$ 上の語といい, その長さ$n$をその長さといい, $n = |x|$ と書く.
$\Sigma$ 上の語全体を$\Sigma ^ \star$で表す.
この記事では桁DPについて扱うので, 特に断らないかぎり$\Sigma = \{0, 1, 2, 3, 4, 5, 6, 7, 8, 9\}$ とします.
次に, 決定性有限オートマトン(以下DFA) を定義します.
定義
決定性有限オートマトン(DFA)とは5項組$M = (Q, \Sigma, \delta, q_0, F)$である. ここで,
- $Q$ は状態からなる空でない有限集合
- $\Sigma$ は認識対象となる入力語に用いられるアルファベット
- $\delta : Q \times \Sigma \to Q$ は動作規制を定める遷移関数
- $q_0 \in Q$ は開始状態
- $F \subset Q$ は受理状態の集合
である.
DFA $M = (Q, \Sigma, \delta, q_0, F)$ が語$w = c_1c_2\cdots c_n \in \Sigma^\star~(c_i \in \Sigma)$ を受理するとは, 次の条件を満たす状態の列$r_0, r_1, \cdots, r_n \in Q$ が存在するときをいう.
- $r_0 = q_0$
- $r_{k+1} = \delta(r_k, c_{k+1})~(k = 0, 1, \cdots, n - 1)$
- $r_n \in F$
語を先頭から順に読み遷移関数に従いながら内部状態を更新していき, すべて読み終えたときの内部状態が受理状態に含まれていれば受理, そうでなければ拒否をするイメージです.
状態を定義だけだとわかりにくいので, 実際に例を見てみましょう. 次のDFA $M$を考えます.
$M = (Q, \Sigma, \delta, q_0, F)$ ここで,
$Q = \{q_0, q_1\}$
$\Sigma = \{0, 1\}$
$\delta : Q \times \Sigma \to Q$ は次の通り :
$q_0$ $q_1$ $0$ $q_1$ $q_1$ $1$ $q_0$ $q_0$
- 開始状態は$q_0$
- 受理状態は$F = \{q_1\}$
$M$ の状態遷移図(各状態$q_i$を頂点とし, $q_j = \delta(q_i, c)~(q_i, q_j \in Q, c \in \Sigma)$ をラベル$c$のついた有向辺$(q_i, q_j)$ で表した有向グラフ)は, 次のようになります.
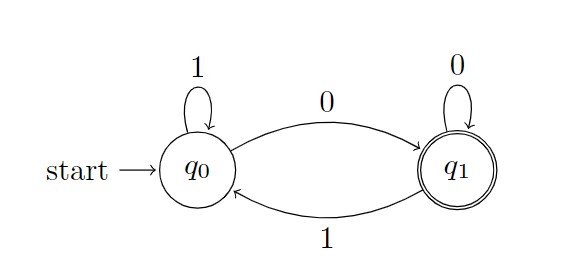
たとえば, このDFA $M$ が$10110$を受理するかどうかを考えます.
$q_0$からスタートし, $q_0, q_1, q_0, q_0, q_1$ の順で遷移していきます. 語をすべて読み終わったときの内部状態は$q_1 \in F$であるため, DFA $M$ は$10110$ を受理することがわかります.
では, $10011$ はどうでしょうか.
$q_0$からスタートし, $q_0, q_1, q_1, q_0, q_0$ と遷移します. 語をすべて読み終わったときの内部状態は$q_0 \notin F$ であるため, DFA $M$ は$10011$ を拒否します.
DFA $M$ は, 偶数を2進数表記したものを受理する機械です.
桁DP
やっと本題です. いくつか問題を見ていきます.
Digits Parade
文字列$S$が与えられます. $S$の各文字は数字($0$~$9$)はか$?$です.
$?$を数字に置き換えてできる整数のうち, $13$で割って$5$あまる数は何通りあるでしょうか? ただし, 頭文字が$0$である場合も整数とみなすものとします.
答えは非常に大きくなる可能性があるため, $10^9+7$で割ったあまりを答えてください.
- $1 \leq |S| \leq 10^5$
$13$で割って$5$あまる数を受理するDFA $M$ を考えます. これは割と簡単に作れます.
$M = (Q, \Sigma, \delta, q_0, F)$ ここで,
$Q = \{q_0, q_1, q_2, \cdots, q_{12}\}$
$\delta : Q \times \Sigma \to Q , (q_i, c) \mapsto q_{(10 \times i + c) \mod 13}$
開始状態は$q_0$
受理状態は$F = \{q_5\}$
$q$の添え字は$13$で割ったときのあまりです. よって開始状態は$q_0$となり, $13$で割って$5$であまる数を受理するため受理状態は$F = \{q_5\}$となります.
たとえば$3376$では, 内部状態は $q_0, q_3, q_7, q_{12}, q_9$ と遷移します. $q_9 \notin F$ であるためDFA $M$は$3376$を拒否します. ここで, $3376 = 259 \times 13 + 9$ です. 終了時の$q$の添え字が$13$で割ったあまりと一致していることがわかります.
受理する例も見てみましょう. $6986 = 537 \times 13 + 5$ では, 内部状態は$q_0, q_6, q_4, q_9, q_5$ と遷移します. $q_5 \in F$であるためDFA $M$ は$6986$を受理します.
$13$で割って$5$あまる数を受理するDFA $M$ が作れました. すると, 問題文を以下のように読み替えることができます.
文字列$S$が与えられます. $S$の各文字は数字($0$~$9$)か$?$です.
$?$を数字に置き換えてできる文字列のうち, DFA $M$が受理するものは何通りありますか?
DP(動的計画法)でこれを解くことを考えます. $S$の$i$文字目(1から数えて)まで見たときに内部状態が$q_j$となるようなものが何通りあるか, を$dp_{i, j}$で表すことにします. また, $S$の$i$文字目を$S[i-1]$と表すことにします(例えば, $S = 12345$としたとき, $S[0] = 1, S[3] = 4$とします).
$dp_{i, j}~(0 \leq i \leq |S|, 0 \leq j < 13)$の初期値を, $$ dp_{i, j} = \begin{cases} 1 & \text{if } i = j = 0\cr 0 & \text{else. } \end{cases} $$ とします. $dp_{0, 0}$ は開始状態です.
$i = 0, 1, \cdots, |S| - 1$について,
-
$S[i] \neq ~?$のとき
$c = S[i]$ とします. 各状態$q_j~(0 \leq j \leq 12)$について, $c$が入力されると$q_{(10 \times j + c) \mod 13}$ へ遷移します. よって, $j = 0, 1, \cdots, 12$ について, $dp_{i+1, (10 \times j + c) \mod 13}$ に$dp_{i, j}$を足していくことにより$dp_{i+1, k}~(0 \leq k \leq 12)$について正しい値が求まります.
-
$S[i] = ~?$のとき
その位置には$0, 1, \cdots, 9$のいずれかが入ります. よって$0, 1, \cdots, 9$すべてについての遷移を考えればよいです.
$c = 0, 1, \cdots, 9$, $j = 0, 1, \cdots, 12$について, $dp_{i+1, (10 \times j + c) \mod 13}$に$dp_{i, j}$を足していくことにより$dp_{i+1, k}~(0 \leq k \leq 12)$について正しい値が求まります.
DFA $M$の受理状態は$F = \{q_5\}$であったので, 求めるべきは$dp_{|S|, 5}$となります.
$10^9+7$で割ったあまりを求めることに注意してください.
// https://github.com/Kyo-s-s/Kyo_s_s_Library/blob/main/md/Modint.md
using Mint = Modint1000000007;
int main(){
string S; cin >> S; // Sを文字列として受け取る
vector<vector<Mint>> dp(S.length() + 1, vector<Mint> (13, 0)); // dp配列を作成 0で初期化
dp[0][0] = 1; // 初期状態
for(int i = 0; i < S.length(); i++){
if(S[i] != '?'){ // S[i]のみ遷移
for(int j = 0; j < 13; j++){
int c = S[i] - '0';
dp[i+1][(10 * j + c) % 13] += dp[i][j];
}
}else{ // 0, 1, ... , 9 のすべてについて遷移
for(int j = 0; j < 13; j++){
for(int c = 0; c < 10; c++){
dp[i+1][(10 * j + c) % 13] += dp[i][j];
}
}
}
}
cout << dp[S.length()][5] << endl;
}
最初なのでDPテーブルがどのような値をとるか確認してみます. たとえば$4?2?$では,
| $i \backslash j$ | $0$ | $1$ | $2$ | $3$ | $4$ | $5$ | $6$ | $7$ | $8$ | $9$ | $10$ | $11$ | $12$ |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| $0$ | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| $1$ | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| $2$ | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 |
| $3$ | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 1 |
| $4$ | 8 | 8 | 7 | 7 | 8 | 8 | 8 | 7 | 8 | 8 | 8 | 7 | 8 |
よって$8$(通り)となります.
このように, 桁DPは「あるDFA $M$が受理するものは何通りか?」という問題に言い換えることができます.
余談
1つ前からしか遷移しないDPのため, このような書き方もできます.
// https://github.com/Kyo-s-s/Kyo_s_s_Library/blob/main/md/Modint.md
using Mint = Modint1000000007;
int main(){
string S; cin >> S;
vector<Mint> dp(13, 0);
dp[0] = 1;
for(auto s: S){
vector<Mint> pd(13, 0);
for(int j = 0; j < 13; j++){
for(int c = 0; c < 10; c++) if(c == s - '0' || s == '?'){
pd[(j * 10 + c) % 13] += dp[j];
}
}
swap(dp, pd);
}
cout << dp[5] << endl;
}
Almost Everywhere Zero
$1$以上$N$以下の整数であって, $10$進法で表したときに$0$でない数字がちょうど$K$個あるようなものの個数をもとめてください.
- $1 \leq N < 10^{100}$
- $1 \leq K \leq 3$
$N$がとても大きいです. 観測可能な範囲の宇宙に存在している原始の数より大きいらしいです(by Wikipedia). こんなに大きい数は数値型では受け取れません. 文字列として受け取ります. 以下, $N$を文字列とし, $0$から数えて$i$番目を$N[i]$と表すことにします(たとえば, $N= 12345$のとき$N[0] = 1, N[4] = 5$です).
まず, $1$以上$N$以下の整数を受理するDFA $M_1$ を考えます. 桁DPの問題ではほとんどの場合, $1$以上$N$以下の整数を受理するDFA $M_1$ が出てきます.
$M_1 = (Q_1, \Sigma, \delta_1, q_{1, 0}, F_0)$. ここで,
$Q_1 = \{q_{1,0}, q_{1,1}, q_{1,2}\}$
$\delta : Q_1 \times \Sigma \to Q_1$ は次の通り: $$ \delta_1(q_{1, 0}, c) = \begin{cases} q_{1, 0} & \text{if } c = N[i]\cr q_{1, 1} & \text{if } c < N[i]\cr q_{1, 2} & \text{else. } \end{cases} ~,~\delta(q_{1, 1}, c) = q_{1, 1},~~\delta(q_{1, 2}, c) = q_{1, 2} $$
初期状態は$q_{1, 0}$
受理状態は$F = \{q_{1, 0}, q_{1, 1}\}$
DFA $M_1$の状態遷移図は次のようになります.
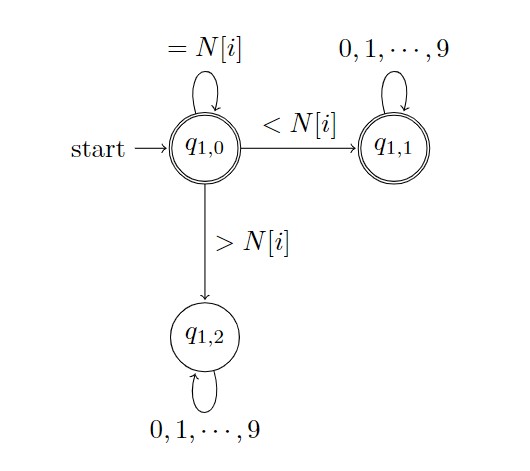
ここで, $i$は今見ているアルファベットが前から何番目か($0$から数えて)を表す変数です.
- $q_0$ : 今まで見てきたアルファベットがすべて$N$と同じ
- $q_1$ : すでに$N$より小さい桁が存在する(=以降はどんなアルファベットが来ても$N$未満)
- $q_2$ : すでに$N$より大きい桁が存在する(=以降はどんなアルファベットが来ても$N+1$以上)
といった感じです(桁DPでよく出てくるsmallerは$q_1$, tightは$q_0$となります).
$N$以下の整数を受理するため, 受理状態は$F = \{q_0, q_1\}$となります.
次に, $10$進法で表したときに$0$でない数がちょうど$K$個であるような数を受理するDFA $M_2$を考えます. 制約より$K = 1, 2, 3$ のときのみを考えればよいです.
$M_2 = (Q_2, \Sigma, \delta_2, q_{2, 0}, F_2)$. ここで,
$Q_2 = \{q_{2, 0}, q_{2, 1}, q_{2, 2}, q_{2, 3},q_{2, 4}\}$
$\delta : Q_2 \times \Sigma \to Q_2$ は次の通り: $$ \delta (q_{2, i}, c) = \begin{cases} q_{2, i+1} & \text{if } (c \neq 0) \land (i < 4)\cr q_{2, i} & \text{else. } \end{cases} $$
初期状態は$q_{2, 0}$
受理状態は$F' = \{q_{2, K}\}$
DFA $M_2$ の状態遷移図は次のようになります(受理状態は$K$によって変わるため書いていません).

添え字は今までに出てきた$0$でない数字の個数です. $K\leq 3$より, $4$つ以上$0$でない数が出てきたらその時点で受理されないため, $q'_4$でループするようにしています.
すると, 問題文を次のように読み替えることができます.
$0, 1, \cdots, 9$からなる$|N|$文字の文字列のうち, DFA $M_1, M_2$がともに受理するものは何通りありますか?
DFA $M_1, M_2$がともに受理する文字列を受理するDFA $M$ を構成します.
DFA $M = (Q, \Sigma, \delta, q_0, F)$ ここで,
- $Q = Q_1 \times Q_2$
- $\delta((q_{1, i}, q_{2, j}), c) = (\delta_1(q_{1, i}, c), \delta_2(q_{2, j}, c))$
- $q_0 = (q_{1, 0}, q_{2, 0})$
- $F = F_1 \times F_2$
とすれば構築できます(DFA $M$が$M_1, M_2$の内部状態をともに保持しているイメージです).
よって, 問題文は次のように読み替えることができます.
$0, 1, \cdots, 9$からなる$|N|$文字の文字列のうち, DFA $M$が受理するものは何通りありますか?
あとはこれをDPで書けばよいです.
int main(){
string N; cin >> N;
int K; cin >> K;
vector dp(N.length() + 1, vector (3, vector<ll> (5, 0)));
dp[0][0][0] = 1;
for(int i = 0; i < N.length(); i++){
for(int j = 0; j < 3; j++){ // M_1
for(int k = 0; k < 5; k++){ // M_2
for(int c = 0; c < 10; c++){
int n = N[i] - '0';
int _j, _k; // 遷移先
if(j == 0){
if(c == n) _j = 0;
else if(c < n) _j = 1;
else _j = 2;
}else{
_j = j;
}
if(c != 0 && k < 4) _k = k + 1;
else _k = k;
dp[i+1][_j][_k] += dp[i][j][k];
}
}
}
}
cout << dp[N.length()][0][K] + dp[N.length()][1][K] << endl;
}
$M_1$について, $q_{1, 3}$へ遷移する場合はその時点でcontinueをしてしまってもよいです(答えに影響しないためです. 普通の桁DPではそもそも$q_{1, 3}$を考えず, $q_{1, 0}$の状態で$c > N[i]$ が来た場合にはcontinueしています). $q_{2, 4}$についても同様のことがいえます.
また, このDPは1つ前からしか遷移しません. それを踏まえてこのような書き方もできます.
int main(){
string N; cin >> N;
int K; cin >> K;
vector dp(2, vector<ll> (4, 0));
dp[0][0] = 1;
for(int i = 0; i < N.length(); i++){
vector pd(2, vector<ll> (4, 0));
for(int j = 0; j < 2; j++) for(int k = 0; k < 4; k++){
for(int c = 0; c < 10; c++){
int n = N[i] - '0';
int _j = j, _k = k;
if(j == 0){
if(c > n) continue;
else if(c < n) _j++;
}
if(c != 0){
_k++;
if(_k == 4) continue;
}
pd[_j][_k] += dp[j][k];
}
}
swap(dp, pd);
}
cout << dp[0][K] + dp[1][K] << endl;
}
jは所謂smallerと同じことをしています(tightはこの逆). 桁DPでよく出てくるこの表現ですが, 実際は$1$以上$N$以下の整数を受理するDFA $M_1$の内部状態を表しています.
この他の桁DP問題
書き足すかもしれません ぽっぽ~


Comment is disabled to avoid unwanted discussions from 'localhost:1313' on your Disqus account...