ABC 255 参加記
クエー 118分6完(5ペナ)で363位、パフォーマンスは1950でした。青2に戻れました!!
A You should output ARC, though this is ABC.
問題
整数$R, C$を$2$行$2$列からなる行列$A$が与えられるので、$A_{R, C}$を出力してね。
- $1 \leq R, C \leq 2$
- $0 \leq A_{i, j} \leq 100$
提出コード
int main(){
int r, c; cin >> r >> c; r--; c--;
vvll A(2, vll(2));
rep(i, 2) rep(j, 2) cin >> A[i][j];
cout << A[r][c] << endl;
}
B Light Lt Up
問題
$xy$平面上に$N$人の人$1, 2, \cdots, N$がいて、人$i$は座標$(X_i, Y_i)$にいます。このうち、$K$人の人$A_1, A_2, \cdots, A_K$に同じ強さの明かりをもたせます。
座標$(x,y)$にいる人が強さ$R$の明かりを持っているとき、その明かりによって中心$(x, y)$、半径$R$の円の内部全体(境界を含む)が照らされます。
すべての人が少なくとも1つのあかりによって照らされるために必要な明かりの強さの最小値をもとめてね。
- $1 \leq K < N \leq 1000$
- $1 \leq A_1 < A_2 < \cdots K< A_K \leq N$
- $|X_i|, |Y_i| \leq 10^5$
- $i\neq j$ならば$(X_i, Y_i) \neq (X_j, Y_j)$
考察
明かりを持っていない人全員に対して、一番近い明かりを持っている人の値を求めれば、それらの$\max$が答えとなります。
提出コード
int main(){
ll N, K; cin >> N >> K;
set<int> A;
rep(i, K){
int a; cin >> a; a--;
A.insert(a);
}
set<int> B;
rep(i, N) if(A.find(i) == A.end()) B.insert(i);
vpll pos(N);
rep(i, N) cin >> pos[i].fi >> pos[i].se;
double ans = 0;
for(auto b: B){
double dist = 10000000000000000;
for(auto a: A){
double x = abs(pos[a].fi - pos[b].fi);
double y = abs(pos[a].se - pos[b].se);
chmin(dist, sqrt(x*x+y*y));
}
chmax(ans, dist);
}
cout << ans << endl;
}
C ±1 Operation 1
問題
整数$X$が与えられます。この$X$に以下を施すことを「操作」と呼びます。
- 以下の$2$つのうちどちらかを選択し、実行する
- $X$に$1$を加算する
- $X$から$1$を減算する
初項$A$、公差$D$、項数$N$の等差数列$S$に含まれる数を「よい数」と呼びます。「操作」を行い$X$を「よい数」にするとき、必要な「操作」の最小回数をもとめてね。
- $-10^{18} \leq X, A \leq 10^{18}$
- $-10^6 \leq D \leq 10^6$
- $1 \leq N \leq 10^{12}$
考察
$S$の最小値は$\min(A, A + (N-1)\times D)$、最大値は$\max(A, A+(N-1)\times D)$です。よって$X$がこの範囲にないとき、$X$は最大値にするか最小値にするかのどちらかになります。よってそれらの操作の回数が少ないときの操作回数を答えればよいです。
$X$がこの範囲にいるとき、適当に操作を行いよい数になるかを判定していきました(本当はもっと簡単にできますが、ペナりまくって焦っていたのでこんなコードになってしまいました…)。
int main(){
ll X, A, D, N; cin >> X >> A >> D >> N;
if(D == 0){
cout << abs(A - X) << endl;
return 0;
}
ll mi = min(A, A + (N-1)*D);
ll ma = max(A, A + (N-1)*D);
ll ans = 0;
if(mi <= X && X <= ma){
ans = INF;
for(ll d = -2000000; d <= 2000000; d++){
if(((X + d) % D + D) % D == (A % D + D) % D && mi <= X+d && X+d <= ma){
chmin(ans, abs(d));
}
}
}else{
ans = min(abs(mi - X), abs(ma - X));
}
cout << ans << endl;
}
$S$の$N$項目を$A + N \times D$にしていて3ペナしてしまったのでもうダメです… こういう問題が出ると頭が壊れてしまいます。もう一度書き直したらWAってしまったのでもう終わりです…
D ±1 Operation 2
問題
長さ$N$の数列$A = (A_1, A_2, \cdots, A_N)$が与えられます。この$A$に以下を施すことを「操作」と呼びます。
- ます、$1 \leq i \leq N$を満たす整数$i$を選択する。
- 次に、以下の$2$つのうちどちらかを選択し、実行する。
- $A_i$に$1$を加算する
- $A_i$から$1$を減算する
$Q$個の質問にこたえてください。$i$番目の質問は、
- 「操作」を$0$回以上何度でも使って$A$の要素をすべて$X_i$にするとき、必要な「操作」の最小回数を求めてね
です。
- $1 \leq N, Q \leq 2 \times 10 ^ 5$
- $0 \leq A_i, X_i \leq 10^9$
考察
まず、$A$と$X$はソートしてよいです。よってソートします($X$はあとでクエリ順に並び替えないといけないのでインデックスも持たせておきます)。
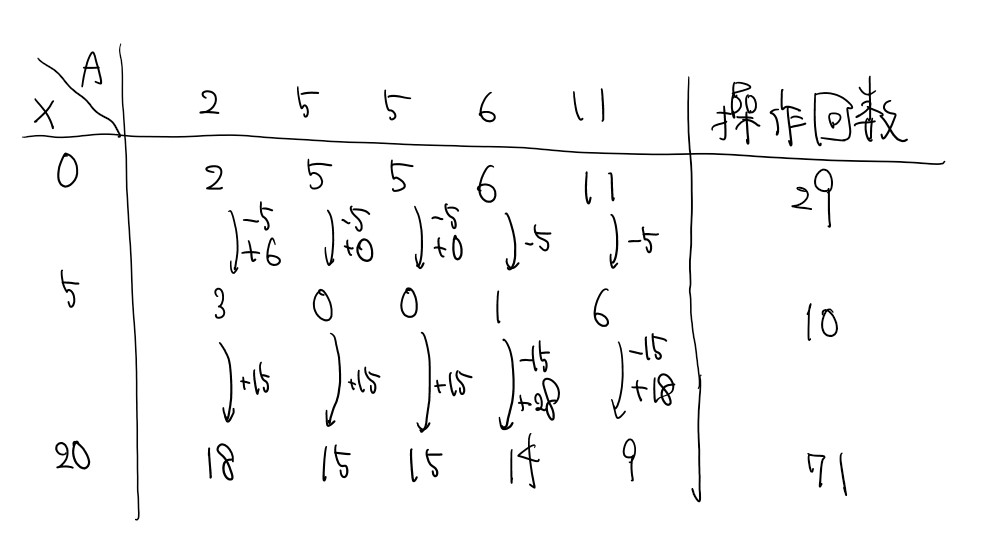
こんな風に値が変化します。ここで、左上の$2$が$3$になっているパートでは、$X$が$5$増えたことにより操作回数が$-5$され$-3$になり、この場合の操作回数は$|-3| = 3$であるため$-3$を$3$にするため$3 \times 2$を足しています。また、この操作が行われた値についてはそれ以降$X$が$x$増えると操作回数が$x$増えます。
こんな感じのことをいい感じにすると通ります。
提出コード
int main(){
ll N, Q; cin >> N >> Q ;
vector<ll> A(N); for(int i = 0; i < N; i++) cin >> A[i];
vpll X(Q);
rep(i, Q){
cin >> X[i].fi;
X[i].se = i;
}
sort(all(A)); sort(all(X));
vpll Ans; //idx, val
int iter = 0; // これより右はXが増えると-される
// これより左はXが増えると+される
ll befx = 0, befa = sum(A);
for(auto [x, i]: X){
ll nxta = befa;
nxta += iter * abs(befx - x);
nxta -= (N - iter) * abs(befx - x);
while(true){
if(iter == N) break;
if(A[iter] - x <= 0){
nxta += abs(A[iter] - x) * 2;
iter++;
}else{
break;
}
}
Ans.pb({i, nxta});
befa = nxta;
befx = x;
}
sort(all(Ans));
for(auto [i, a]: Ans) cout << a << endl;
}
E Lucky Numbers
問題
長さ$N-1$の整数列$S = (S_1, S_2, \cdots, S_{N-1})$及び、「ラッキーナンバー」として $M$個の相異なる整数$X_1, X_2, \cdots, X_M$が与えられます。長さ$N$の整数列$A = (A_1, A_2, \cdots, A_N)$であって、次の条件を満たすものを「よい数列」と呼びます。
すべての$i = 1, 2, \cdots, N-1$について、$A_i + A_{i+1} = S_i$が成り立つ。
よい数列$A$を1つ選ぶ時の$A$の要素のうちラッキーナンバーであるものの個数(すなわち$A_i \in \{X_1, X_2, \cdots, X_M\}$となる$1$以上$N$以下の整数$i$の個数)としてあり得る最大値を求めてね。
- $2 \leq N \leq 10^5$
- $1 \leq M \leq 10$
- $-10^9 \leq S_i, X_i \leq 10^9$
- $X_1 < X_2 < \cdots < X_M$
考察
$A_1$を決めるとすべての$A$が決まります。また、$A_1$を$1$増やすと偶数番目の$A$は$+1$され、奇数番目の$A$は$-1$されます。よって、$A_1 = 0$の時の$A$を求めてから、$i = 2,3, \cdots, N, j = 1, 2, \cdots, M$について$A_i$を$X_j$にするためにするべき$A_1$の値を求め、それを数えていきます。
$A_1$がラッキーナンバーの時の処理を忘れて1WAしましたが、うまく実装すればそんなこと起こりえないですね 反省… ただ考察パートは爆速で済んですぐコーディングに移れたので成長を感じます。
提出コード
int main(){
ll N, M; cin >> N >> M;
vector<ll> A(N-1); for(int i = 0; i < N-1; i++) cin >> A[i];
vector<ll> X(M); for(int i = 0; i < M; i++) cin >> X[i];
map<ll, int> score;
// 0 にした時を求める
vll AA = {0};
for(auto a: A){
AA.pb(a - AA.back());
}
for(int i = 1; i < N; i++){
int k = (i % 2 == 0) ? -1 : 1;
for(auto x: X){
ll add = (x - AA[i]) * k;
score[add]++;
}
}
int ans = 0;
for(auto [k, v]: score){
for(auto x: X) if(k == x) v++;
chmax(ans, v);
}
cout << ans << endl;
}
F Pre-order and In-order
問題
$1, 2, \cdots, N$と番号づけられた$N$個の頂点を持つ二分木を考えます。頂点$1$を根とする二分木であり、書きの条件を満たすものが存在するか判定し、存在するならばその一例を示してください。
- DFSしたときの行きがけ順が$P$
- DFSしたときの通りがけ順が$I$
- $2 \leq N \leq 2 \times 10^5$
- $P, I$は$(1,2, \cdots, N)$の順列
考察
サンプル1を見ます。$P = 1,3,5,6,4,2 , ~~I = 3,5,1,4,6,2$です。$P$の1番目は$1$であるため、$1$の左に$3, 5$が、右に$4, 6, 2$が来ます。これを再帰的にやっていきます。$3, 5$の中で$P$に出現するのが一番早いのは$3$であるため$3$の右の子が$5$であることがわかり… と繰り返していきます。つまり、通りがけ順が$I$になるように$P$の出現するインデックスの小さいものから確定させていきます。 最後に、この手順で作った木の行きがけ順が$P$と一致するかを確認し、一致したらそれを出力します。RMQをするためにセグ木を持ってきましたが、解説ではそんなことをせずにやっていたのでもしかしたら嘘解法かもしれません。
提出コード
#include <atcoder/all>
using namespace atcoder;
using S = int;
S op(S a, S b){ return min(a, b); }
S e(){ return 100000000; }
int main(){
ll N; cin >> N;
vector<ll> P(N); for(int i = 0; i < N; i++) cin >> P[i];
vector<ll> I(N); for(int i = 0; i < N; i++) cin >> I[i];
vll appear(N + 1);
rep(i, N) appear[P[i]] = i + 1;
vi Ip(N + 1);
rep(i, N) Ip[i + 1] = appear[I[i]];
segtree<S, op, e> seg(Ip);
vpii Ans(N+1, {0, 0});
vi ipos(N + 1);
rep(i, N) ipos[I[i]] = i + 1;
bool ans = true;
auto solve = [&](auto&& self, int x, int l, int r) -> void {
// xの位置 -> ipos[x]
int as = seg.prod(l, r);
if(x != P[as - 1]){
ans = false; return;
}
// 左の子存在する場合
if(l != ipos[x]){
int api = seg.prod(l, ipos[x]);
Ans[x].fi = P[api-1];
self(self, P[api-1], l, ipos[x]);
}
// 右の子存在する場合
if(ipos[x]+1 != r){
int api = seg.prod(ipos[x]+1, r);
Ans[x].se = P[api-1];
self(self, P[api-1], ipos[x]+1, r);
}
};
solve(solve, 1, 1, N+1);
vll rute;
auto dfs = [&](auto&& self, int now) -> void {
rute.pb(now);
if(Ans[now].fi != 0) self(self, Ans[now].fi);
if(Ans[now].se != 0) self(self, Ans[now].se);
};
dfs(dfs, 1);
if(rute != P) ans = false;
if(ans){
rrep(i, N){
cout << Ans[i].fi << " " << Ans[i].se << "\n";
}
}else{
cout << -1 << endl;
}
}


Comment is disabled to avoid unwanted discussions from 'localhost:1313' on your Disqus account...