ABC 248 参加記

2022.04.17

競技プログラミング

72分6完(1ペナ)で299位、2034パフォでした。初黄パフォ＆入青！わーい！

入青記事はこちらです。

A Lacked Number

問題

数字のみからなる、長さがちょうど9の文字列$S$が与えられます。$S$には0から9までのうち、ちょうど1つの数字を除いた9種類の数字が1度ずつ登場します。$S$に登場しない唯一の数字を出力してください。

$S$は数字のみからなる長さ9の文字列

$S$の文字はすべて相異なる

提出コード

int main(){

    string S; cin >> S;
    
    map<int, int> cn;

    for(auto s: S) cn[s - '0']++;

    rep(i, 10) if(cn[i] == 0) cout << i << endl;
    
}

B Slimes

問題

$A$匹のスライムがいます。すぬけくんが1回叫ぶたびにスライムは$K$倍に増殖します。スライムが$B$匹以上になるには、すぬけくんは最小で何回叫ぶ必要がありますか？

$1 \leq A \leq B \leq 10^9$

$2 \leq K \leq 10^9$

提出コード

int main(){

    ll A, B, K; cin >> A >> B >> K;
    
    ll ans = 0;

    while(true){
        if(A >= B) break;
        ans++;
        A *= K;
    }

    cout << ans << '\n';

}

C Dice Sum

問題

長さ$N$からなる数列$A = (A_1, \cdots, A_N)$であって、以下の条件を満たすものは何通りありますか？

$1 \leq A_i \leq M ~(1 \leq i \leq N)$

$\displaystyle \sum_{i = 1}^N A_i \leq K$

ただし、答えは非常に大きくなることがあるので、答えを 998244353 で割った余りを求めてください。

$1 \leq N, M \leq 50$

$N \leq K \leq NM$

考察

別に考察記事を書こうと思っています。よってここでは省略します。

提出コード

// https://github.com/Kyo-s-s/Kyo_s_s_Library/blob/main/lib/math/modint.cpp
using Mint = Modint998244353;

int main(){

    ll N, M, K; cin >> N >> M >> K;

    vector<Mint> dp(K + 1);
    dp[0] = 1;

    rep(i, N){
        vector<Mint> pd(K + 1);
        rep(k, K + 1){
            for(int add = 1; add <= M; add++){
                if(k + add < K + 1){
                    pd[k + add] += dp[k];
                }
            }
        }
        swap(dp, pd);
    }

    Mint ans = 0;
    rep(i, K + 1) ans += dp[i];
    cout << ans << endl;

}

D Range Count Query

問題

長さ$N$の数列$A = (A_1, \cdots, A_N)$が与えられます。　$Q$個のクエリにこたえてください。

L R X : $A_L, \cdots, A_R$のうち、値が$X$に等しいものの個数を求めよ。

$1 \leq N \leq 2 \times 10 ^ 5$

$1 \leq A_i \leq N$

$1 \leq Q \leq 2 \times 10^5$

各クエリについて、$1 \leq L \leq R \leq N,~1 \leq X \leq N$

考察

$1, 2, \cdots, N$について、数列$A$の何番目に出現するか？を配列で持っておきます。すると、クエリL R Xでは、$X$について($R+1$以上が初めて出現するインデックス) $-$ ($L$以上が初めて出現するインデックス) を答えればよいので1つのクエリを$O(\log N)$でさばけます。

提出コード

int main(){

    ll N; cin >> N;
    vector<ll> A(N); for(int i = 0; i < N; i++) cin >> A[i];
    
    vector<vector<ll>> app(N + 1);

    rep(i, N){
        ll a = A[i];
        app[a].pb(i + 1);
    }

    ll Q; cin >> Q;
    rep(q, Q){
        ll L, R, X; cin >> L >> R >> X;
        
        ll l = bisect_left(app[X], L);
        ll r = bisect_left(app[X], R + 1);
        cout << r - l << endl;

    }
}

E K-colinear Line

問題

座標平面上の$N$個の点が与えられます。$1\leq i \leq N$について、$i$番目の点の座標は$(X_i, Y_i)$です。座標平面上の直線であって、$N$個の点のうち$K$個以上の点を通るものの個数を求めてください。そのような直線が無限に存在する場合はInfinityを出力してください。

$1 \leq K \leq N \leq 300$

$|X_i|, |Y_i| \leq 10^9$

$i \ne j$ならば$X_i \ne X_j$または$Y_i \ne Y_j$

考察

$K = 1$のとき、答えはInfinityです。それ以外の時、答えがInfinityになることはありません。$K \geq 2$の時を考えます。

直線を方程式で表そうとするととても大変です(浮動小数点で持つと誤差でダメになってしまいます。分数で持つのも分数ライブラリがないと大変です)。

$N$個の点のなかから2点を選ぶと、その2点を通る直線が1つだけ存在します(同じ点は存在しないため)。2点を先に決めてしまい、その2点を通る直線上にある点を探します。$K$個以上あったら答えに1を加算し、同一直線上にある点を重複して数えないようにメモしておきます。これをすると解けます。メモにsetを使ってしまいましたが、2次元配列で持った方が無駄な$\log$がつかずにキレイですね。

提出コード

/*3点が同一線上にあるか？　*/
bool isonLine(ll x1, ll y1, ll x2, ll y2, ll x3, ll y3){
    ll dx1 = x1 - x2;
    ll dy1 = y1 - y2;
    ll dx2 = x1 - x3;
    ll dy2 = y1 - y3;
    return dx2 * dy1 == dx1 * dy2;
}

int main(){

    ll N, K; cin >> N >> K;
    vpll XY(N);
    rep(i, N) cin >> XY[i].fi >> XY[i].se;

    set<pll> ok;
    
    if(K == 1){
        cout << "Infinity" << endl; exit(0);
    }

    ll ans = 0;

    rep(i, N) rep(j, N){
        if(i == j) continue;
        if(ok.find({i, j}) != ok.end()) continue;

        vll arr = {i, j};
        rep(k, N) if(i != k && j != k){
            if(isonLine(XY[i].fi, XY[i].se, XY[j].fi, XY[j].se, XY[k].fi, XY[k].se)){
                arr.pb(k);
            }
        }

        if(arr.size() >= K) ans++;

        rep(s, arr.size()) rep(t, arr.size()) ok.insert({arr[s], arr[t]});
    }

    cout << ans << '\n';
    
}

F Keep Connect

問題

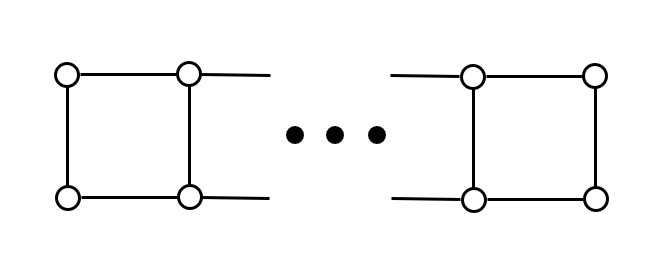
2以上の整数$N$および素数$P$が与えられます。下図のような$2N$頂点$(3N-2)$辺のグラフ$G$を考えます。

$i = 1, 2, \cdots, N - 1$について、次の問題を解いてください。

$G$の$3N-2$本の辺からちょうど$i$本の辺を取り除く方法であって、辺を取り除いた後のグラフも連結であるようなものの個数を$P$で割ったあまりを求めよ。

$2 \leq N \leq 3000$

$9 \times 10^8 \leq P \leq 10^9$

$P$は素数

考察

$N \leq 3000$なので、$O(N^2)$が通ります。ここでDPじゃないかなぁという推測を立てます(問題もDPっぽいので)。実際DPで解くことができます。

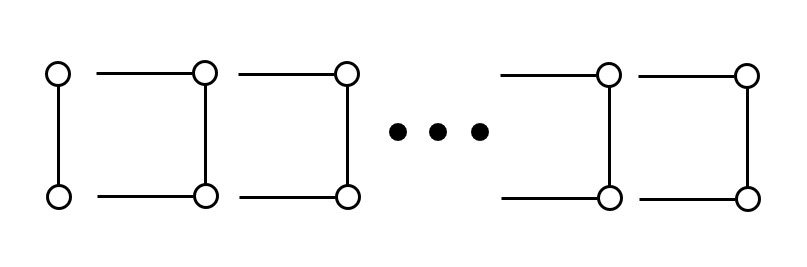
ABC248img2

このように分解し、左から右へ見ていきます。DPテーブルを、$dp[j][k] :=$ $j$本の辺を取り除いて、今見ている右端の上と下が連結か？(連結なら$k = 1$、連結でないなら$k = 0$)とします。遷移を考えます。まずは右端の上と下が連結の場合です。

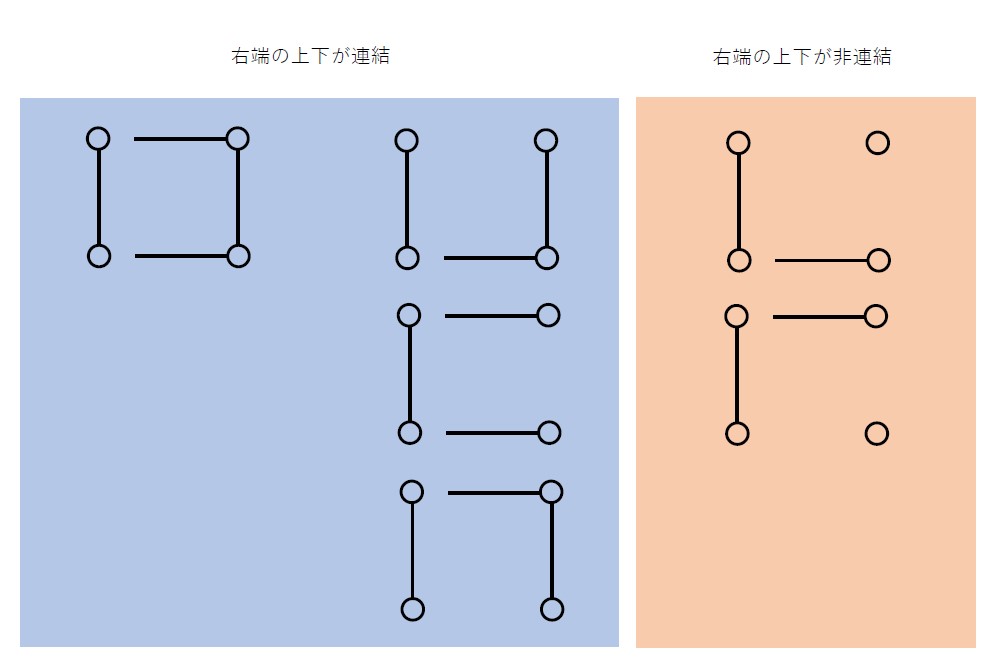
ABC248img3

左から0本、1本、2本取り除いた場合の条件を満たすつなげ方です。0本、1本取り除いた場合は上下が連結のままですが、2本取り除いた場合は上下が連結でなくなります。

次に右端の上と下が連結でない場合です。

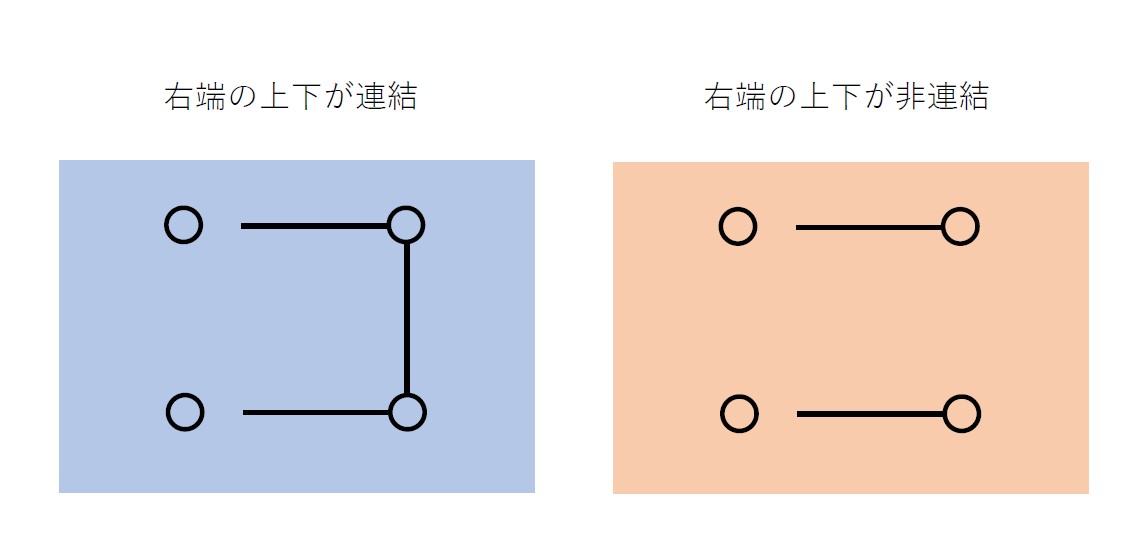
ABC248img4

左から0本、1本取り除いた場合の条件を満たすつなげ方です。2本取り除くことはできません(非連結な部分ができてしまいます)。

これで遷移をすべて出すことができました。

素数$P$がテストケースによって変わるので、ACLのmodintを使いました。

提出コード

#include <atcoder/all>
using namespace atcoder;
using mint = modint;

int main(){

    ll N, P; cin >> N >> P;
    mint::set_mod(P);

    vector dp(N + 10, vector<mint> (2, 0));
    //取り除いた数、上と下が連結か 連結-> 1
    dp[0][1] = 1;
    dp[1][0] = 1;

    //コの字はN-1個
    rep(o, N - 1){
        vector pd(N + 10, vector<mint> (2, 0));
        rep(i, N + 1){

            //非連結
            pd[i + 0][1] += dp[i][0];
            pd[i + 1][0] += dp[i][0];

            //連結
            pd[i + 0][1] += dp[i][1];
            pd[i + 1][1] += 3 * dp[i][1];
            pd[i + 2][0] += 2 * dp[i][1];
            
        }
        swap(dp, pd);
    }

    rrep(i, N - 1){
        cout << dp[i][1].val();
        if(i == N) cout << endl;
        else cout << " ";
    }
}

1つ前からのみ遷移するDPはこのようにswapしていくと添え字が1つ減って楽になります。